AuraQ has vast experience helping organisations find the gaps that can be filled to enhance their business. This could be to improve efficiency, integrate legacy systems or deliver new portals and strategic applications to create competitive advantage. Contact us to request a free, no obligation Gap Analysis.
Distance calculations using latitudes and longitudes
Recently, we’ve been working with maps and location data and required the use of some distance calculations. These were particularly useful for determining the closest destination/s from a list to a single origin and helping with planning and optimising routes between locations. We were given the latitude and longitude of a set of locations on a map, representing stops along waste collection routes. We were interested in the effect of adding an extra location to this set and how this might affect existing routes. This could help to determine whether servicing this new stop on the route would be feasible and profitable. Below are some of the calculations we used.
Bounding box
Firstly, we needed to narrow down a list of locations to those within a certain distance (in kilometres) of a new point, i.e. those within 5 km of this new point. This is simply to narrow down the list of points we are working with, thus reducing the number of calculations required later. The simplest method for this is to calculate the coordinates of a bounding box at a certain distance around the new point.
The corners of the bounding box give us the maximum and minimum values for latitude and longitude, which we will use to find all points satisfying the following inequalities:
Min Latitude <= Latitude <= Max Latitude
Min Longitude <= Longitude <= Max Longitude
We could have used a bounding circle for this problem, however this would be inefficient. For example, if we had 100 locations to filter down, using a circle we would have to calculate the distance between the new point and each existing point, before selecting all points where this distance is below a certain value. In this example we would need 100 calculations, whereas using a bounding box allows us to use only four calculations before executing the data retrieve.
To calculate the bounding box coordinates, we find the length of one degree of longitude in kilometres and likewise find the length of one degree of latitude in kilometres. Using this it becomes simple to convert the kilometre distance into degrees of latitude and longitude away from the new point. Degrees of latitude remain almost constant, whereas, degrees of longitude vary greatly. Suppose we have a set of coordinates (X1,Y1), where X1 is the latitude and Y1 is the longitude. Degrees of latitude vary from 110.574 km at the equator to 111.694 km at the poles. One degree of latitude can be approximated to 111 km for our calculations. Hence, the latitude of a point d kilometres away will be:
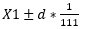
Degrees of longitude vary much more greatly from 111.320 km at the equator to 0 km at the poles. The approximation for 1 degree of longitude = cos(Latitude)*degree length of longitude at the equator. Hence, the latitude of a point d kilometres away will be:
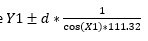
Using these equations, we can generate four new points surrounding the original. (Min Latitude, Min Longitude), (Max Latitude, Min Longitude), (Min Latitude, Max Longitude) and (Max Latitude, Max Longitude). These are the coordinates of the bounding box around the original point. We are interested in any points whose latitude is between the minimum and maximum and whose longitude is also between the minimum and maximum.
Haversine formula
The bounding box allows us to determine whether a point is within a certain distance of another point but does not provide us with the value of the distance between the two points. For this we need to use the Haversine formula. The Haversine formula finds great circle distance between two points given their latitudes and longitudes. “The great-circle distance or orthodromic distance is the shortest distance between two points on the surface of a sphere, measured along the surface of the sphere (as opposed to a straight line through the sphere’s interior)”. This formula allows us to determine how close two points are and make comparisons between these distances. To find this distance, we simply enter the latitude and longitude of our two points into the following Haversine formula:
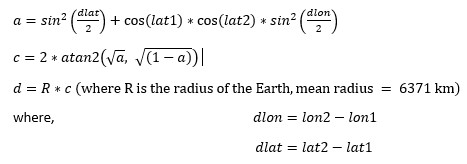
Google driving distance
In order to analyse realistic driving routes that include the new location, we need to know driving distances between locations. Google’s Distance Matrix API provides information on travel time and distance, documented here: https://developers.google.com/maps/documentation/distance-matrix/intro We provide a single origin with multiple destinations, given by their latitude and longitude. This returns the distance between the origin and each destination. The API will allow multiple origins and multiple destinations, returning the distances between each origin and destination combination. We’ve utilised this API as a way of comparing distances from one location, to each location in a list. Below is an example response for driving distances from Worcester to Liverpool and Birmingham:

Summary
Distance calculations can be extremely useful when working with location data. The above calculations provided methods of manipulating the data and comparing distances with the accuracy we required. Depending on the distance chosen for the bounding box calculations, some locations with shorter driving distances may have been discarded, but this can be set to a suitably large value as to include most of the relevant data. Once we’d used the bounding box calculation to narrow the initial list of locations to a certain area, we were then able to analyse routes accurately using the other two distance calculations.